Matrix Multiplication Help |
|
Matrix Multiplication
Before you can even attempt to perform matrix multiplication, you must be sure that the last dimension of the first matrix is the same as the first dimension of the second matrix.
You can multiply a 2x3 matrix times a 3x1 matrix but you can not multiply a 3x1 matrix times a 2x3 matrix. The dimension of the matrix resulting from a matrix multiplication is the first dimension of the first matrix by the last dimenson of the second matrix. Multiplying a 2x3 matrix times a 3x1 matrix yields a 2x1 matrix. Multiplying a 3x4 matrix times a 4x2 matrix yields a 3x2 matrix. The product of two matrices is found by adding the row elements multiplied times the column elements. Example 1:
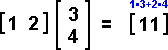 Note: (1x2)•(2x1) → (1x1) matrix.Example 2:
 Note: (2x2)•(2x1) → (2x1) matrix.Example 3:
 Note: (2x1)•(1x3) → (2x3) matrix.Determinant of a Matrix
In order to find the determinant of a matix, the matrix must be square, i.e. 2x2, 3x3, 4x4, nxn.
The determinant of a 2x2 matrix is the product of the down diagonal [ \ ] minus the product of the up diagonal [ / ]. Note how the determinant uses bars instead of brackets. Example 4:
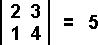 (2•4)-(1•3) = 8-3 = 5The determinant of a 3x3 matrix can be quite involved, however, the computation can be simplified considerably using the following procedure:
Copy the first two columns of the matrix immediately to the right of the existing matrix. Compute the product of each of the down diagonals and add them all together. Compute the product of each of the up diagonals and add them all together. The determinant is equal to the sum of the down diagonal products minus the sum of the up diagonal products. Procedure :
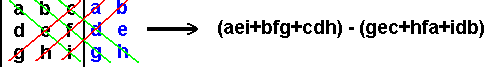 Example 5:
Down Diagonals: (2)•(4)•(-3) + (3)•(-2)•(3) + (-1)•(2)•(1) = (-24)+(-18)+(-2) = -44
Up Diagonals: (3)•(4)•(-1) + (1)•(-2)•(2) + (-3)•(2)•(3) = (-12)+(-4)+(-18) = -34 Down Diagonals - Up Diagonals: (-44) - (-34) = -44 + 34 = -10 Inverse of a Matrix
Only square matrices can have an inverse; i.e. 2x2, 3x3, etc.
The inverse of a matix multiplied by the original matrix, will result in the identity matrix. The inverse of a 1x1 matrix is simply the reciprical of the single entry in the matrix; eg. [5]-1 = [1/5] and [5]•[1/5] = [1]. The inverse of a 2x2 matrix can be found by using the following formula: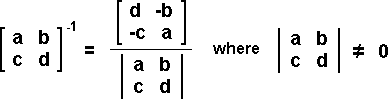 
Since division by zero is not allowed, the determinant of the matrix cannot be zero. The inverse is not defined whenever the determinant of the matrix equals zero. A zero determinant will occur whenever the second row of the matrix is a multiple of the first row.
Since the determinant is a unique number, the formula basically tells you to divide every term in the resultant matrix by that unique number. Note that the numerator of the inverse matrix switches the first row, first term and the last row, last term while the other two terms are simply negated in place. Example 6:
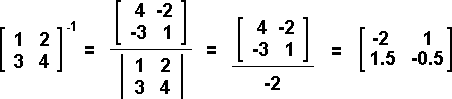
Finding the inverse of a larger matrix can be quite time consuming unless you have a calculator that can perform this task; however, it can be done manually.
One of the simplest ways is to augment the identity matrix to the right of the matrix that you wish to invert and then perform row operations that will transform your original matrix into the identity matrix with the matrix inverse assuming the position of your augmented identity matrix. This is best illustrated with an example. Example 7:
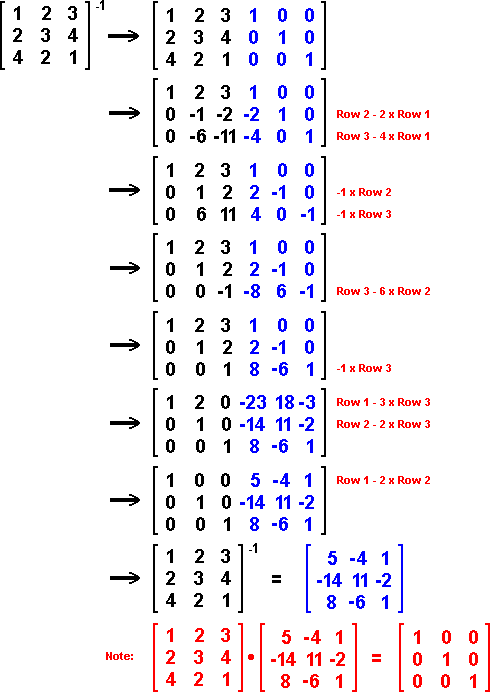
This method will work for any nxn matrix. Remember that if the determinant of the matrix equals zero, the inverse does not exist.
|
