Slope Equation Help

Subject Areas

Tools / Misc

bCalc

drag-N-drop

scrnGC2: Calc Input

scrnGC3: f(x) Plot Input

scrnGC4: g(x) Plot Input

The inputs above will be hidden when the program finally gets launched. Currently, I am not hiding them even when you close the calculator. The purpose of the inputs is to help in debugging. This allows you to enter simple code on the calculator screen but the program translates the input to javascript math. Give it a try and see if you notice any obvious problems or have suggestions for improvements.

gCalc

drag-N-drop

Select precision* of answer:

Select angle mode:

Enter expression to evaluate here:

The answer is shown below:

Enter function to be plotted:

f(x) =

Enter 2nd function, if needed:

g(x) =

Change or reset the x-y scaling below:

x_min =

x_max =

y_min =

y_max =

Accuracy Disclaimer

The javascript math object methods used for this calculator are not accurate for very large or very small numbers. In particular, the trigonometric functions may yield very small answers that should actually be zero or very large answers that should be infinite. This typically occurs at 90� or pi/2 intervals.

DO NOT USE WHERE HIGH PRECISION IS REQUIRED. USE AT YOUR OWN RISK.

(Close Window)

Slope Equation Help

Calculate the Slope of a Line

The simplest way to calculate the slope of a line passing through 2 points is to set up a small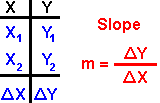
"T-Chart" as shown below:

It doesn't matter which point is in which row. Subtraction of the bottom row from the top row will give you the change in y and the change in x. The ratio of the change in y divided by the change in x is the slope. This is commonly referred to as the rise over the run.

Example 1:
The slope of the line passing through the points (5,12) and (1,4) is 2.

Slope-Intercept Form

The slope-intercept form of a linear equation is in the form: y = mx + b.

The slope-intercept form is one of the easiest forms to understand and to graph. The only information required to write slope-intercept form of a linear equation are the slope and the y-intercept. If the slope is not given, it can be calculated as shown above. If the slope and y-intercept are given, the equation can be written directly with no further calculation.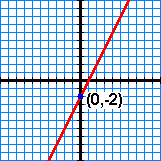

Example 2:
Given a slope of 2 and a y-intercept of 0,-2
the equation can be written as y = 2x - 2.

If the slope and one point are given, but the point is not the y-intercept, then the y-intercept can be calculated by using the y = mx + b formula.

Example 3:
Given a slope of 3 passing through (1,6),
6=3(1)+b
6=3+b → b=3
y = 3x + 3

Point-Slope Form

The point slope form of a linear equation is in the form: y - y₁ = m ( x - x₁ )

The slope-intercept form is very easy to use when you are given a point and a slope.

For example 3, the point-slope form of the equation is: y - 6 = 3 ( x -1 )

Generally, one can switch between the various forms by simply rearranging an equation.

Standard Form

The standard form of a linear equation is in the form: Ax + By + C = 0, where A, B and C are integers.

If you are able to write the point-slope form of a linear equation then you can derive the standard form simply by moving all the variables and constants to the same side of the equation.

For example 2, the standard form of the equation is: 2x - y - 2 = 0

For example 3, the standard form of the equation is: 3x - y + 3 = 0

Occasionally, the slope may not be a whole number in which case you will need to multiply the entire expression by the smallest number that will get rid of any fractions or decimals.

For example: 0.5x - y + 3 = 0 multiplied by 2 yields x - 2y + 6 = 0.