Pyramid Volume Measure Help

Subject Areas

Tools / Misc

bCalc

drag-N-drop

scrnGC2: Calc Input

scrnGC3: f(x) Plot Input

scrnGC4: g(x) Plot Input

The inputs above will be hidden when the program finally gets launched. Currently, I am not hiding them even when you close the calculator. The purpose of the inputs is to help in debugging. This allows you to enter simple code on the calculator screen but the program translates the input to javascript math. Give it a try and see if you notice any obvious problems or have suggestions for improvements.

gCalc

drag-N-drop

Select precision* of answer:

Select angle mode:

Enter expression to evaluate here:

The answer is shown below:

Enter function to be plotted:

f(x) =

Enter 2nd function, if needed:

g(x) =

Change or reset the x-y scaling below:

x_min =

x_max =

y_min =

y_max =

Accuracy Disclaimer

The javascript math object methods used for this calculator are not accurate for very large or very small numbers. In particular, the trigonometric functions may yield very small answers that should actually be zero or very large answers that should be infinite. This typically occurs at 90° or pi/2 intervals.

DO NOT USE WHERE HIGH PRECISION IS REQUIRED. USE AT YOUR OWN RISK.

(Close Window)

Pyramid Volume Measure Help

Volume Formulas for Pyramids

Regular Square Pyramid
Volume = 1/3 • ( area of the base ) • height
Volume = 1/3 • b ² • height
V = 1/3 • b ² • h

Regular Hexagonal Pyramid
Volume = 1/3 • ( area of the base ) • height
Volume = 1/3 • 6 • √ 3 • ( b / 2 ) ² • height
V = √ 3 • b ² • h / 2

Hexagonal pyramid base area details are shown below.

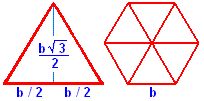
The hexagon base is made up
of six equalateral triangles, as
shown at the far right.

One such triangle has been
enlarged to show further detail.

The base, b has been divided in half to illustrate that the height of the triangle is b / 2 • √ 3.

Note: The distance from the base to the center of the regular polygon is referred to as the apothem.

Given the base and height of the triangle one can calculate the area of one triangle as:

Area of one triangle = ( b / 2 ) • ( b / 2 • √ 3 ) = b ² • √ 3 / 4

The area of the base is equal to six of the area computed,

Base Area = 6 • b ² • √ 3 / 4 = 1.5 • b ² • √ 3